对数函数性质有哪些？记住这五条考试肯定用得上。

今天没事，就想着重新拾掇拾掇以前学过的东西，翻到对数函数这块儿。感觉很多性质有点模糊，索性就动手实践一下，加深点印象。

回忆与实践

我先从最基本的定义开始想。对数函数，一般写成 y = logx 这种形式。当时学的时候记得有几个条件，底数a得大于0还不能等于1，真数x必须大于0。这个x > 0特别关键，直接决定这函数的定义域。

光记定义没啥意思，我就找个稍微复杂点的例子来练手，试试求定义域。比如这个函数 y = log(2x-1)。按照定义，我得一步步来：

• 看底数，这里的底数是x。那根据规矩，x > 0 并且 x ≠ 1。
• 再看真数，是 (2x-1)。这个整体必须大于0，也就是 2x - 1 > 0。

然后我就解这两个不等式。2x - 1 > 0 解出来是 x > 1/2。好，现在要把所有条件合在一起看：又要 x > 0，又要 x ≠ 1，还要 x > 1/2。我把这几个条件在脑子里或者纸上画个数轴比划一下，很明显，的范围就是 x > 1/2 并且 x ≠ 1。这么一动手算，定义域这块儿就清楚多。

接着我想到值域。这个对数函数y的值能取到多少？我印象里好像是全体实数。试着想想，当x很大很大时，y也能很大；当x很小很小，接近0的时候，y就能变成很小的负数（如果a>1的话）。它的值域应该是整个实数集R，没啥上下限。

画图与观察

然后我试着回忆一下它的图像。对数函数的图像都挺有特点的，我记得它们都会过一个固定的点。是哪个点来着？对，是(1, 0)。因为不管底数a是啥（只要符合规定），log1 永远等于0。这个点是焊死在图像上的。

图像的走势跟底数a很有关系。我记得分两种情况：

• 当a > 1的时候，比如logx，我脑补一下或者随手画个草图，发现x越大，y也越大，图像是往上走的，这是单调递增的。



• 当0 < a < 1的时候，比如logx，情况就反过来，x越大，y反而越小，图像是往下降的，这是单调递减的。

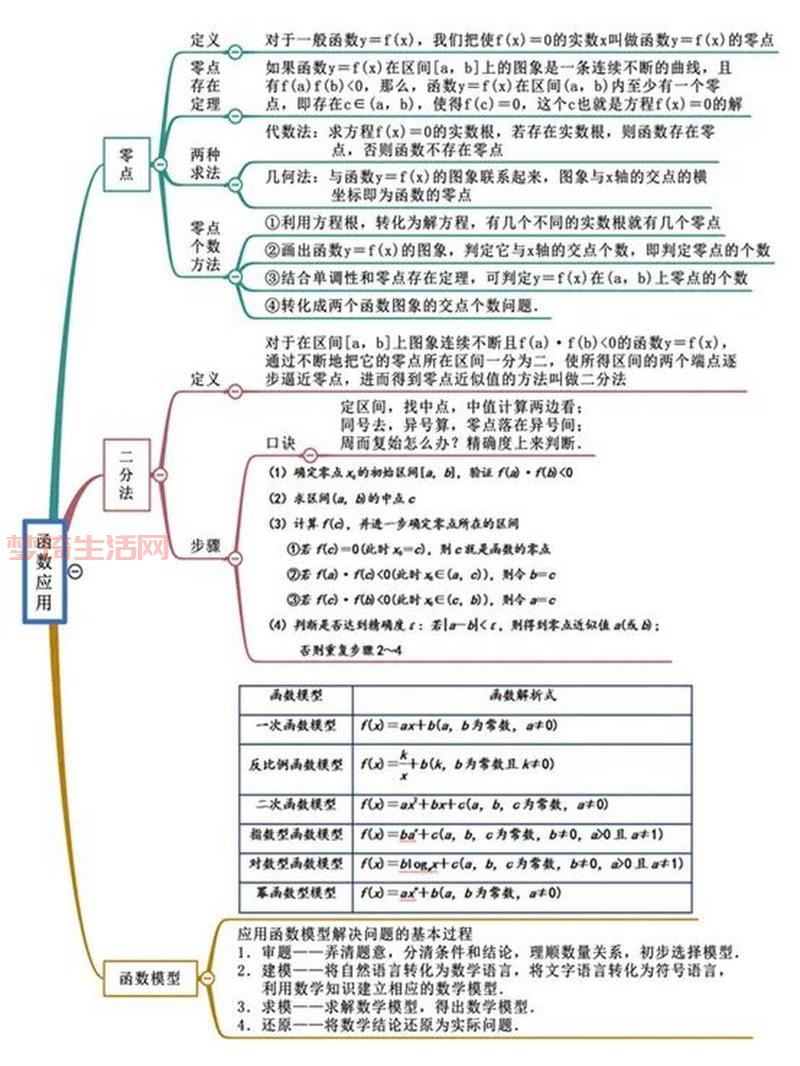
这个单调性还挺重要的，比较大小啥的经常用到。

其他零碎性质

我还顺带想想其他的性质：

• 奇偶性：我看看图像，它既不对称于y轴，也不对称于原点。所以它肯定不是奇函数也不是偶函数，是个非奇非偶的家伙。
• 周期性：图像一直那么走，没有重复循环的段落，所以没有周期性。
• 最值：因为值域是R，所以它既没有最大值也没有最小值。
• 零点：函数图像和x轴的交点，就是y=0的时候，前面说，就是那个定点(1,0)，所以零点是x=1。

我还特别提醒自己一下，就是那个老生常谈的问题：负数和0是没有对数的！这个是基础中的基础，计算和求定义域时绝对不能忘。

就这么一步步回忆、动手算、画图想，感觉对对数函数的性质又熟悉一遍。实践一遍确实比干看书印象深刻多。