合数的定义原来如此简单，小学生也能轻松学会！

今天没事儿，就想着捣鼓一下数学里头那个“合数”到底是啥玩意儿。之前老是听人说质数、合数什么的，有点迷糊，索性自己动手查查，搞明白它。

我就翻翻手边的资料，也上网随便搜搜。看到好几种说法，有点绕。有的说什么“除1和本身，还能被别的数整除”，有的说什么“有两个以上的大于1的因数乘积”，还有的说“至少有三个因数”。看得我头都大点。

摸索过程

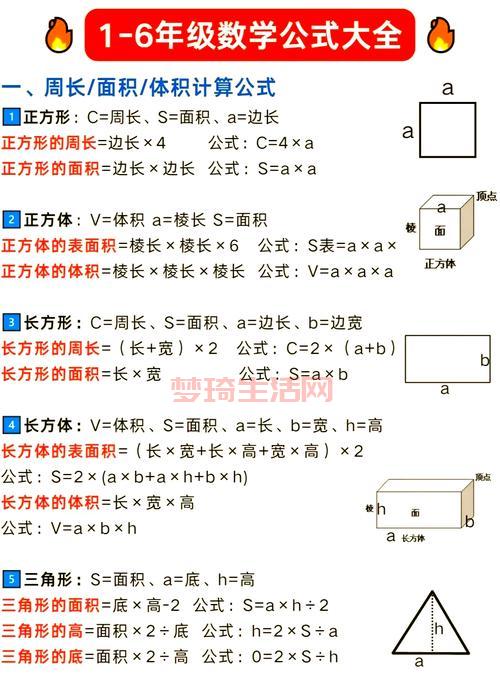
我就想，得找个简单的法子理解。我先从“因数”这个词下手。一个数的因数，说白就是能整除这个数的那些整数。比如，6，能被1整除，能被2整除，能被3整除，也能被6整除。那么1、2、3、6就是6的因数。

然后我再回头看合数的定义，就好理解多。

• 第一步：看定义核心。核心就是，一个数，如果除1和它自己这两个因数之外，还有其他的因数，那它就是合数。
• 第二步：找例子验证。 我就试几个数：

  

  • 比如数字 4。它的因数有1、2、4。你看，除1和4，它还有个因数2。4就是合数。
  • 再比如数字 6。它的因数有1、2、3、6。除1和6，还有2和3。6也是合数。
  • 还有数字 9。它的因数有1、3、9。除1和9，还有个3。9也是合数。
  • 像 10，因数是1、2、5、10。有2和5这两个额外的因数，妥妥的合数。



• 第三步：排除特殊情况。 我注意到定义里老强调“大于1的整数”。那 1 算啥？1的因数只有1它自己。它既不满足“只有1和本身两个因数”（质数的定义），也不满足“除1和本身还有其他因数”（合数的定义）。1既不是质数，也不是合数。这个得记牢。
• 第四步：对比质数。 为加深理解，我又想想质数。质数是就是只有1和它本身两个因数的数，比如2（因数1、2），3（因数1、3），5（因数1、5），7（因数1、7）。这么一比，合数就是“不纯粹”的数，它的因数比较多，至少得有三个（1，本身，还有一个其他的）。

搞明白

这么一步步捋下来，我就彻底搞明白。

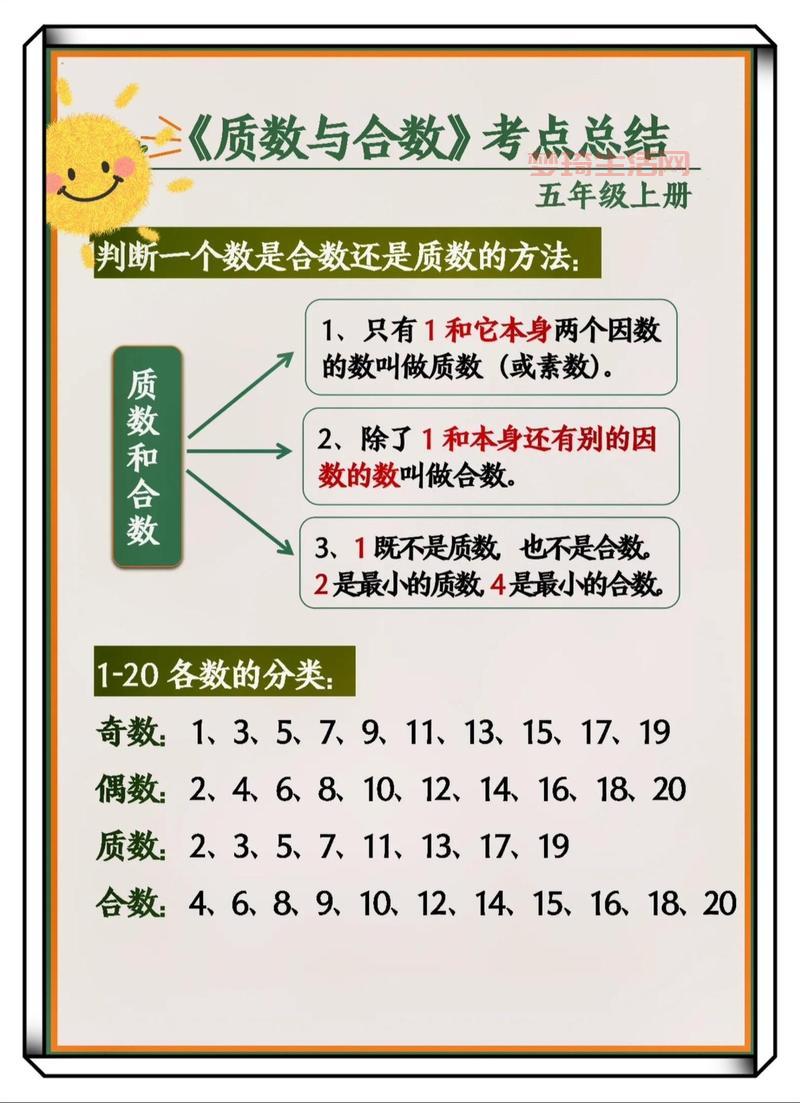
合数，简单说，就是一个大于1的整数，除能被1和它自己整除外，还能被别的整数整除。 或者用因数的说法，一个大于1的整数，如果它的因数个数超过两个（也就是至少有三个因数），那它就是合数。

最小的合数就是4。所有大于2的偶数，因为都能被2整除，所以它们除1和本身外，至少还有个因数2，所以大于2的偶数肯定都是合数。

今天这个实践过程还挺有意思的，把一个模糊的概念自己动手给琢磨清楚，感觉不错。下次再碰到合数，心里就有底。